| Difficult | Execution Time | Data Analysis | Radioactive Sources |
|---|---|---|---|
| No | Gamma |
Hardware setup
This experiment guide is referred to the SP5620CH educational kit. If you don’t have this kit, choose your own from the following list to visualize the related experiment guide:
Equipment
- SP5620CH – Cosmic Hunter
Purpose of the experiment
Statistical properties of the cosmic rays.
Fundamentals
The event number in a given time interval is one of the most interesting points in many Physics phenomena. This number is often affected by statistical fluctuations around an average value determined by the type of phenomenon. Multiple factors may cause fluctuations and influence the measurement result. Thus, the exact value is not always the same (as in the case of particles that decay may derive from space or from a radioactive source).
The most important goal in the experimental approach is to understand which values can occur in a series of measurements as well as their probability, i.e. the probability distribution. The Poisson distribution describes with good approximation events comings from radioactive phenomena or from counting cosmic rays. This distribution expresses the probability of a given number of events occurring in a fixed interval of time or space, and can be expressed as:
Pµ(n) = (µn / n!) * e–µ
where µ is the average number of events in a fixed interval and n is the number of events.
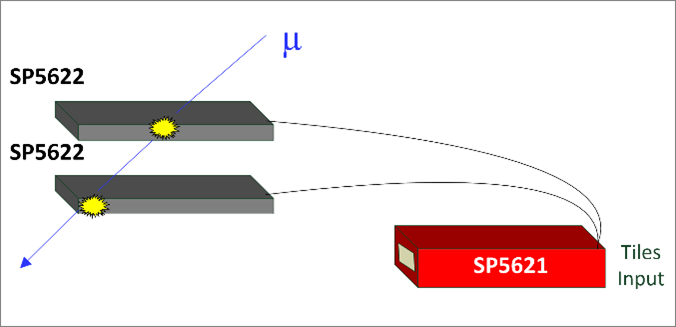
Experimental setup block diagram
Carrying out the experiment:
Connect the cable connector from each SP5622 Detection System to the input located on the rear panel of of the SP5621 module. Power on the SP5621 module and start acquisition via the START button on the front panel. When a charged particle crosses the black tile its energy is converted into scintillation light. The photons produced are detected by the photosensor and converted into an electrical signal. The number of counts for each scintillator is available via the SP5621 display. Note that spurious electrical signals will likely also be detected by the photosensor, thus producing noise. Coincidence between two SP5622 will greatly reduce the number of spurious events. However, the statistical fluctuations cannot be totally removed. Select the scintillators coincidence via the related button on the front panel, then select the integration time of the measurement. Before starting acquisition choose the system geometry. Be sure to keep this geometry constant for the duration of the experiment. Take and record more data to obtain statistical significance.
Results:
The Poisson distribution of cosmic rays can be experimentally verified via data analysis and the treatment of their statistical uncertainty.
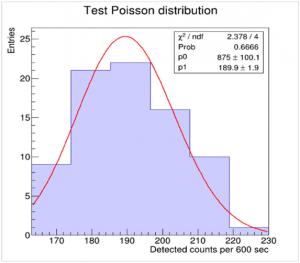
Poissonian distribution of cosmic rays [Fit: y = p0* (p1x/x!)*e-p1]


