| Difficult | Execution Time | Data Analysis | Radioactive Sources |
|---|---|---|---|
  |
  |
Yes | No |
Hardware setup
This experiment guide is referred to the SP5600D/AN educational kit. If you don’t have this kit, choose your own from the following list to visualize the related experiment guide:
SG6213D – Cosmic Hunter
Equipments:
SP5600D/AN – Beta Kit
An additional SP5608 – Scintillating tile is required
Purpose of the experiment
To understand the potential for accidental counts coming from double tile coincidence.
Fundamentals
Once the geometry of the detectors has been defined and coincidence is confirmed it becomes important to estimate the number of random coincidences. Random coincidences derive from simultaneous or nearly-simultaneous pulses caused by accidental discharges (i.e. noise), and not by particles with a trajectory within the volume determined by the solid angle of the geometry. The probability that a particle crosses the detector is a function of the surface of the tile itself and of the average rate. Therefore, the probability of a random coincidence is proportional to the pulse duration.
An evaluation of random coincidence contribution [Rrandom] can be obtained by a simple theoretical calculation, Janossy method based [RD6]:
Rrandom = 2*RA*RC*τ
Where τ is the pulse duration (700 ns), and RA and RC are the event rate of each scintillating tile.
Carrying out the experiment
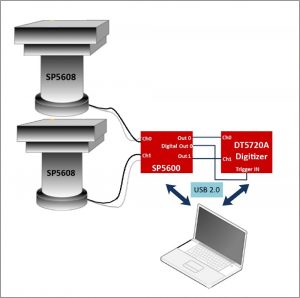
Experimental setup block diagram.
Before starting acquisition choose the system geometry. Be sure to keep this geometry constant for the duration of the experiment. Take and record more data to obtain statistical significance.
Results
Double tile coincidence plays a key role in a great many Physics experiments. The random coincidence rate allows you to evaluate the data quality via estimation of the Signal to Background ratio [SBR].
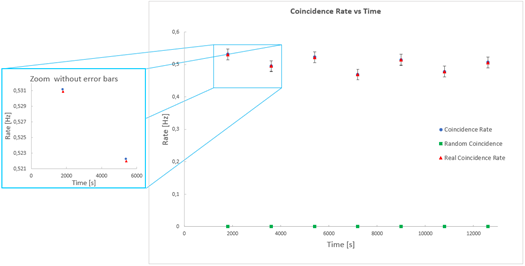
Trend of the Count Rate and Random Rate as a function of the time. The plot on the left side is an enlargement of the main plot and underlines the deviation between the measured coincidence rate and the real one, obtained via the random rate subtraction.
