| Difficult | Execution Time | Data Analysis | Radioactive Sources |
|---|---|---|---|
| Yes | No |
Hardware setup
This experiment guide is referred to the SP5600EMU Emulation Kit. If you don’t have this kit, choose your own from the following list to visualize the related experiment guide:
- SP5630EN/P – Enviromental Kit
- SP5600C/AN – Gamma Kit
- SP5650 – Open FPGA Kit
- SP5640 – Backpack Detector
Equipment
- SP5600EMU – Emulation Kit
Purpose of the experiment
Study the statistical distribution of the counting rates of a gamma radioactive source.
Comparison of the data to the Poisson distribution, turning into a Gaussian as the mean number of counts grows. The study can be performed both experimentally, with the SiPM kit or simulating it with the emulation kit.
Fundamentals
The number of radioactive particles detected over a time Δt is expected to follow a Poisson distribution with mean value μ. It means that for a given radioactive source, the probability that n decays will occur over a given time period Δt is given by:
![]()
Where μ is proportional to the sample size and to the time Δt and inversely proportional to the half-life T1/2 of the unstable nucleus. As long as μ grows, the probability P μ(n) is well approximated by a Gaussian distribution:
![]()
Where σ = √μ is the standard deviation.
Carrying out the experiment
To perform the experiment connect the DT4800 output to the input channel of the MCA DT5770 and use the DT4800 GP0 as digitizer “trigger IN”. The DT4800 Control Software Interface allows to generate exponential decay signals with programmable rise time and fall time and it is possible to emulate signals from a real energy spectrum linked to a radioactive source with variable activity.
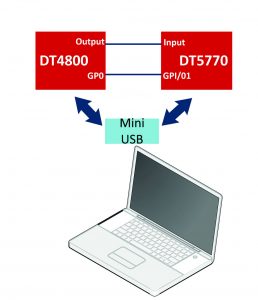
Block diagram of the experimental setup that makes use of the “Emulation Kit”
Results
Changing the counting window and/or the activity of the source or the threshold, the number of counts changes, with a probability density function moving form a Poissonian to a Gaussian shape. The student may play with the data, fitting them and comparing the expectations to the measurement.
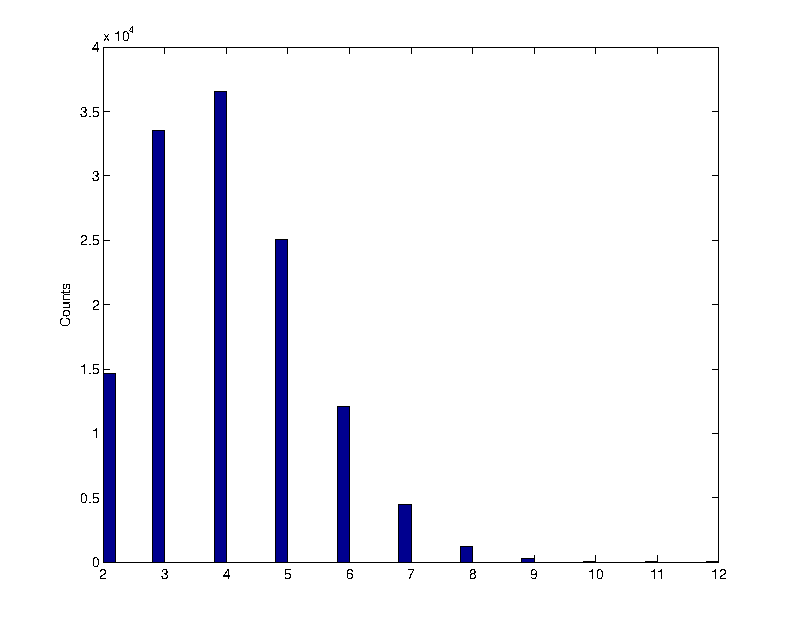
Poissonian distribution
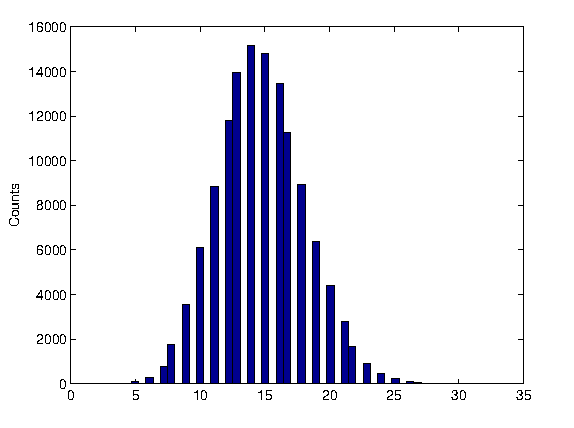
Gaussian distribution


