| Difficult | Execution Time | Data Analysis | Radioactive Sources |
|---|---|---|---|
  |
  |
Yes | Yes |
Hardware setup
This experiment guide is referred to the SP5640 Backpack detector kit. If you don’t have this kit, choose your own from the following list to visualize the related experiment guide:
- SP5630EN/P – Enviromental Kit
- SP5600C/AN – Gamma Kit
- SP5650 – Open FPGA Kit
- SP5600EMU – Emulation Kit
Equipment
- SP5640 – Backpack Detector
- Additional Gamma Radioactive Source
Purpose of the experiment
Study the statistical distribution of the counting rates of a gamma radioactive source. Comparison of the data to the Poisson distribution, turning into a Gaussian as the mean number of counts grows. The study can be performed both experimentally, with the SiPM kit or simulating it with the emulation kit.
Fundamentals
The number of radioactive particles detected over a time Δt is expected to follow a Poisson distribution with mean value μ. It means that for a given radioactive source, the probability that n decays will occur over a given time period Δt is given by:
Pμ(n) = (μn / n!)*eμ
Where μ is proportional to the sample size and to the time Δt and inversely proportional to the half-life T1/2 of the unstable nucleus. As long as μ grows, the probability Pμ(n) is well approximated by a Gaussian distribution:
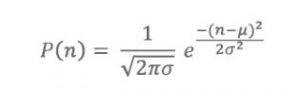
Where 
is the standard deviation.
Carrying out the experiment
The experiment can be performed both by taking off the instrumentation from the backpack and using the backpack with the open zipper. To power ON γstream, press the ON/OFF button. Take care that the γstream internal battery is charged, otherwise use the external power system. Connect the Ethernet cable from γstream to the PC and configure the Ethernet network of your PC. Connect γstream to the MC2Analyzer software through Ethernet connection. Run the software and power ON the detector. Place the radioactive source close to the scintillator/under the central part of the backpack to perform the experiment.
Results
Changing the counting window and/or the activity of the source or the threshold, the number of counts changes, with a probability density function moving form a Poissonian to a Gaussian shape. The student may play with the data, fitting them and comparing the expectations to the measurement.
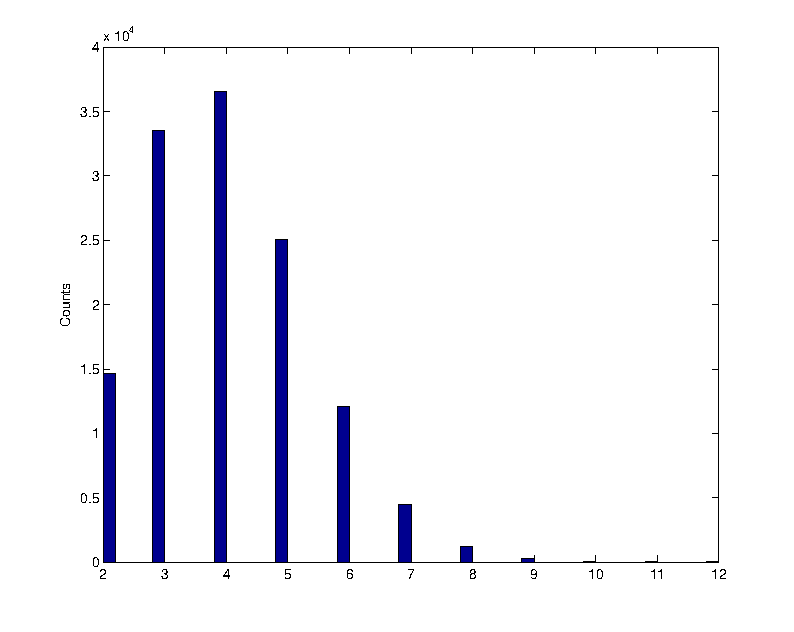
Poisson distribution
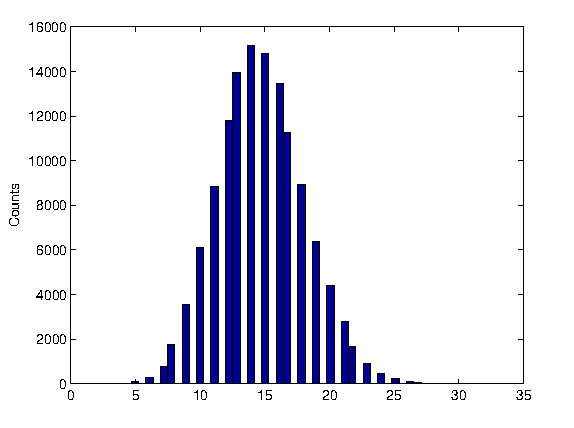
Gaussian distribution
